客服微信：gaokaoquan678
知识点总结
本节主要包括抛物线的定义、抛物线定义的简单应用、抛物线标准方程的形式、抛物线标准方程的求法、抛物线的简单几何性质、抛物线的简单应用等知识点。其中主要是理解和掌握抛物线线的简单几何性质，理解和掌握它最好的方法是通过数形结合。
1、抛物线的定义
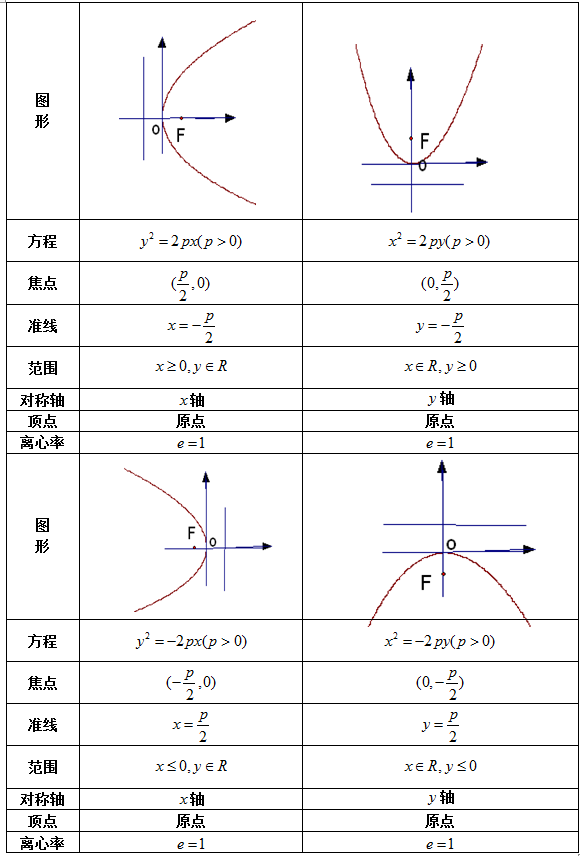
2、抛物线的标准方程和简单的几何性质
3、求抛物线的标准方程
一般用待定系数法，先定位，后定量。如果不能确定，要分类讨论。
常见考法
在段考中，多以选择题、填空题和解答题的形式考查抛物线的简单几何性质。选择题和填空题一般属于容易题，解答题一般属于难题。在高考中，一般以解答题的形式融合其它圆锥曲线联合考查抛物线的几何性质，难度较大。
误区提醒
1、求抛物线的方程，用待定系数法，先定位，后定量。不确定时要分类讨论。
2、如果抛物线中，涉及抛物线上的点到焦点的距离或涉及焦点弦，一般可考虑使用抛物线的定义，使用几何法求解，比使用方程组要简单。
【典型例题】
例1 A、B是抛物线y2＝2px(p>0)上的两点，且OA⊥OB.
(1)求A、B两点的横坐标之积和纵坐标之积；
(2)求证：直线AB过定点；
(3)求弦AB中点P的轨迹方程；
(4)求△AOB面积的最小值．
解：设A(x1，y1)，B(x2，y2)，中点P(x0，y0)．
例2 已知抛物线C：y2＝2px(p>0)过点A(1，－2)．
(1)求抛物线C的方程，并求其准线方程；
解：(1)将(1，－2)代入y2＝2px，得(－2)2＝2p·1，所以p＝2，故所求抛物线C的方程为y2＝4x，其准线方程为x＝－1.
(2)假设存在符合题意的直线l，其方程为y＝－2x＋t，
